在實務上存續期間有兩種常用的計算方式，一種是馬考雷存續期間（Macaulay Duration），另一種是修正存續期間（Modified Duration）。馬考雷存續期間是由Frederick Macaulay在1938年所提出，後人依此命名。存續期間衡量某張債券的持有人平均在多少時間後可以拿回債券的配息和本金。Macaulay的債券存續時間用的平均是加權平均。每個支付的利息和本金都有一個加權值，而這個權值等於該利息或本金的現值占債券現值的比例。修正存續期間和馬考雷存續期間不同，單位不是年，但它也是用來衡量如果利率變化1%，債券價格預期會改變多少，計算公式是用麥考利存續期間算出來的數字/（1+到期殖利率/年配息次數）。

其計算方式舉例如下：

假設某債券票面金額是10,000，票面利率2%，六年後到期，到期殖利率是3%：

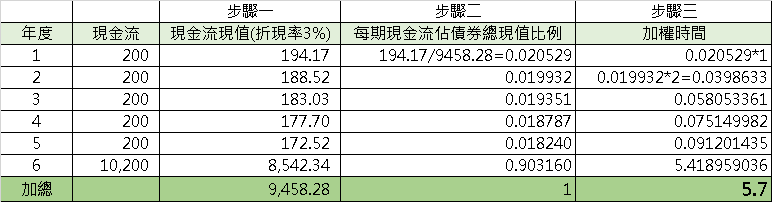
依照步驟就可計算出存續期間為5.7年，意思是市場利率每變動1%，債券價格預期會變動5.7%。

另一種則是修正存續期間，和麥考利存續期間不同，單位不是年，但它也是用來衡量如果利率變化1%，債券價格預期會改變多少，計算公式是用麥考利存續期間算出來的數字/（1+到期殖利率/年配息次數）。

例如上面那個案例，麥考利存續期間是4.8年，到期殖利率3%、年配息次數1次，那麼它的修正存續期間就是：5.7/（1+0.03/1）=5.53

這代表如果市場利率上升1%，債券價格預估會下跌5.53%，不過這是估計值而已，實際狀況如果利率變動越大，用修正存續期間來預估會越不準確。

比較馬考雷存續期間和修正存續時間

由於馬考雷存續期間衡量投資者必須持有債券直到債券現金流的現值等於為債券支付的金額的加權平均時間，因此債券基金經理人經常使用它來通過債券免疫策略（Immunization）管理債券投資組合風險。

相比之下，修正存續期間確定了收益率每百分比變化的存續期間變化量，同時衡量利率變化對債券價格的影響程度。因此，修正存續期間可以通過估算債券價格隨著利率上升而下降的幅度，因此多使用來為債券投資者提供風險衡量標準。

本介紹所含訊息，係依據一般市場交易慣例所撰擬，僅供參考，並不代表中國信託綜合證券股份有限公司之意見，且不保證所提供資料及數據之準確性或全面性。本介紹之目的並非針對買賣證券、選擇權、期貨或其他證券相關商品提供推介服務，亦非進行交易之要約，個人或企業之理財決策仍需依自身財務能力、投資知識、風險承受能力等因素自行獨立判斷決定，並承擔相關風險及損益結果，，任何人不得以因信賴本介紹之內容及資料而做出決策或投資為由，向本公司主張任何權利及提出訴訟。本介紹之著作權屬本公司所有，非經本公司同意，任何人不得將本介紹加以引用或轉載。